SET IDENTITIES
Sets: $P,Q,R$
Universal Set $I$
Compliment:$P^{'}$
Proper subset: $P\subset Q$
Empty Set $\phi$
Union of sets: $P\cup Q$
Intersection of sets: $P\cap Q$
Difference of sets: $P\setminus Q$
1. $P\subset I$
2. $P\subset P$
3. $P=Q$ if $P\subset Q$ and $Q\subset P$
4. Empty Set
$\phi \subset P$
5. Union of Sets
$R=P\cup Q=\{x|x\in P\:or\: x\in Q \}$
6. Commutativity
$P\cup Q=Q\cup P$
7. Associative
$P\cup (Q\cup R)=(P\cup Q)\cup R$
8. Intersection of Sets
$C=P\cap Q=\{x|x\in P\:and\: x\in Q \}$
9. Commutativity
$P\cap Q=Q\cup P$
10. Associative
$P\cap (Q\cap R)=(P\cap Q)\cap R$
11. Distributivity
$P\cup (Q\cap R)=(P\cup Q)\cap (P\cup R)$
$P\cap (Q\cup R)=(P\cap Q)\cup (P\cap R)$
12. Idempotency
$P\cap P=P$
$P\cup P=P$
13. Domination
$P\cap \phi=\phi$
$P\cup I=I$
14. Identity
$P\cup \phi=P$
$P\cap I=P$
15. Compliment
$P^{'}=\{x\in I|x\not\in P\}$
16. Compliment of Intersection and Unions
$P\cup P^{'}=I$
$P\cap P^{'}=\phi$
17. De Morgan's Laws
$(P\cup Q)^{'}=P^{'}\cap Q^{'}$
$(P\cap Q)^{'}=P^{'}\cup Q^{'}$
18. Difference of Sets
$R=Q\setminus P=\{x|x\in Q\: and \: x\not\in P\}$
19. $Q\setminus P=Q\setminus (P\cap Q)$
20. $Q\setminus P=Q\cap P^{'}$
21. $P\setminus P=\phi$
22. $P\setminus Q=P\:if\:P\cap Q=\phi$
23. $(P\setminus Q)\cap R=(P\cap R)\setminus (Q\cap R)$
24. $P^{'}=I\setminus P$
25. Cartesian Product
$R=P\times Q=\{(x,y)|x\in P\: and\: y\in Q\}$
SETS OF NUMBERS
Natural Number:$N$
Whole Number:$N_{0}$
Integer:$Z$
Positive Integer:$Z^{+}$
Negative Integer:$Z^{-}$
Rational Integer:$Q$
Real Integer:$R$
Complex Numbers:$C$
26. Natural Numbers
Counting Numbers:$N=\{1,2,3,...\}$
27. Whole Numbers
Counting Numbers and zero:$N_{0}=\{0,1,2,3,...\}$
28. Integers
Whole numbers and their opposites and zero:
$Z^{+}=N=\{1,2,3,...\},$
$Z^{-}=N=\{...,-3,-2,-1\},$
$Z=Z^{-}\cup \{0\}\cup Z^{+}=\{...,-3,-2,-1,0,1,2,3,...\}$
29. Rational Numbers
Repeating or terminating decimals:
$Q=\{x|x=\frac{a}{b}\: and\: a\in Z\: and\: b\in Z\:and\: \neq 0\}$
30. Irrational Numbers
Nonrepeating and nonterminating decimals:
$Q^{'}=\{x|x\neq\frac{a}{b}\: and\: a\in Z\: and\: b\in Z\:and\: \neq 0\}$
31. Real Numbers
Union of rational and irrational numbers:
$R=Q\cup Q^{'}$
32. Complex Numbers
$C=\{x+iy|x\in R\: and\: y\in R\},$
where i is the imaginary unit.
33. $N\subset Z\subset Q\subset R\subset C$
BASIC IDENTITIES
Real Numbers:$a,b,c$
34. Additive Identity
a+0=a
35. Additive Inverse
a+(-a)=0
36. Commutative Of Addition
a+b=b+a
27. Associative Of Addition
(a+b)+c=a+(b+c)
38. Definition Of Subtraction
a-b=a+(-b)
39. Multiplicative Identity
a.1=a
40. Multiplicative Inverse
$a.\frac{1}{a}=1,a\neq 0$
41. Multiplication Times 0
a.0=0
42. Commutative Of Multiplication
a.b=b.a
43. Associative Of Multiplication
(a.b).c=a.(b.c)
44. Distributive Law
a(b+c)=ab+ac
45. Definition of Division
$\frac{a}{b}=a.\frac{1}{b}$
COMPLEX NUMBERS
Natural number:n
Imaginary Number:i
Complex Number:z
Real part:a,c
Imaginary part:bi,di
Modulus of a complex number:$r,r_{1},r_{2}$
Argument of a complex number:$\theta,\theta_{1},\theta_{2}$
46.
$i^{1}=i\quad\: i^{5}=i \quad\quad i^{4n+1}=i\\
i^{2}=-1\quad i^{6}=-1 \quad i^{4n+2}=-1\\
i^{3}=-i\quad i^{7}=-i \quad i^{4n+3}=-i\\
i^{4}=1\quad\: i^{8}=1 \quad\quad i^{4n}=1$
47. z=a+bi
48. Complex Plane
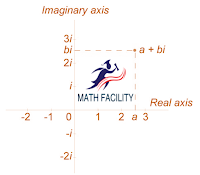
49. (a+bi)+(c+di)=(a+c)+(b+d)i
50. (a+bi)-(c+di)=(a-c)+(b-d)i
51. (a+bi)(c+di)=(ac-bd)+(ad+bc)i
52. $\frac{a+bi}{c+di}=\frac{ac+bd}{c^{2}+d^{2}}+\frac{bc-ad}{c^{2}+d^{2}}i$
53. Conjugate Complex Numbers
$\overline{a+bi}=a-bi$
54. $a=rcos\theta ,b=rsin\theta$
55. Polar Presentation of Complex Numbers
$a+bi=r(cos\theta+isin\theta$
56. Modulus and Argument of a complex Number
If a+bi is a complex number, then
$r=\sqrt{a^{2}+b^{2}}$(modulus),
$\theta=arctan\frac{b}{a}$(argument).
57. Product in Polar Representation
$z_{1}z_{2}=r_{1}(cos\theta_{1}+isin\theta_{1}).r_{2}(cos\theta_{2}+isin\theta_{2})$
$=r_{1}r_{2}[cos(\theta_{1}+\theta_{2})+isin(\theta_{1}+\theta_{2})]$
58. Conjugate Numbers in Polar Representation
$\overline{r(cos\theta+isin\theta)}=r[cos(-\theta)+isin(-\theta)]$
59. Inverse of a Complex Number in Polar Representation
$\frac{1}{r(cos\theta+isin\theta)}=\frac{1}{r}[cos(-\theta)+isin(-\theta)]$
60. Quotient In Polar Representation
$\frac{z_{1}}{z_{2}}=\frac{r_{1}(cos\theta_{1}+isin\theta_{1})}{r_{2}(cos\theta_{2}+isin\theta_{2})}=\frac{r_{1}}{r_{2}}[cos(\theta_{1}-\theta_{2})+isin(\theta_{1}-\theta_{2})]$
61. Power of a Complex Number
$Z^{n}=[r(cos\theta+isin\theta)]^{n}=r^{n}[cos(n\theta)+isin(n\theta)]$
62. Formula "DE Moivre"
$(cos\theta+isin\theta)^{n}=cos(n\theta+isin(n\theta)$
63. Nth Root of a Complex Number
$\sqrt[n]{z}=\sqrt[n]{r(cos\theta+isin\theta)}=\sqrt[n]{r}(cos\frac{\theta+2\pi k}{n}+isin\frac{\theta+2\pi k}{n})$
where k=0,1,2,...,n-1
64. Euler's Formula
$e^{ix}=cosx+isinx$